往复泵介杆的有限元分析方法

介杆是往复泵中连接活塞杆与十字头的重要零件。通过分析介杆的结构特点及受力情况，基于ANSYS 有限元分析软件平台，利用不同加载方式对其进行强度分析，并结合理论计算结果，提出了介杆有限元分析的合理方法。

前言

介杆(见图1)是往复泵中连接十字头与活塞杆的重要零件，其右侧大端面通过螺栓与十字头联接在一起，左侧靠卡箍与活塞杆连接。通过分析介杆的应力分布及*大应力值，计算其**系数，可以校核零件的强度是否满足使用要求，并为优化设计提供理论依据。

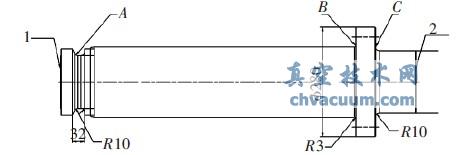
图1 介杆示意图

1. 活塞杆端 2. 十字头端

本文通过对比介杆在不同加载方法下的应力结果，结合理论计算，提出了介杆有限元分析的相关建议，为介杆的合理分析提供了帮助。

1、介杆的有限元分析

(1)十字头端约束法

由于介杆为对称式结构，所以采用1/4 模型分析：在对称面施加对称约束；在与十字头联接面施加轴向约束；在与活塞杆联接面施加相当于135 t的压力，得到的有限元模型如图2 所示。

图2 介杆有限元模型

(2)活塞杆端约束法

采用1/4 模型分析：在对称面施加对称约束；在与活塞杆联接面施加轴向约束；在与十字头联接面施加相当于135 t 的压力，得到的有限元模型如图3所示。

图3 介杆有限元模型

(3)装配体分析法

采用十字头、介杆、与活塞杆装配体的1/2 模型分析，视活塞杆与介杆为一体(即联接面上的节点一致)，在活塞杆与十字头接触面设置接触；在对称面施加对称约束；在十字头与下滑板接触处施加径向约束；在活塞杆左侧端面施加轴向约束；在十字头销孔处施加相当于135 t 的余弦力， 得到的有限元模型如图4 所示。

图4 装配体有限元模型

(4)计算结果

根据上述分析方法，A、B、C 3 处应力值对比如表1 所示。可以看出，3 种计算方法对A 处应力值影响不大。十字头端约束法与装配体分析法的B 处和C 处的应力值较为接近， 且与第1 种计算方法差距较大。

表1 有限元分析结果对比

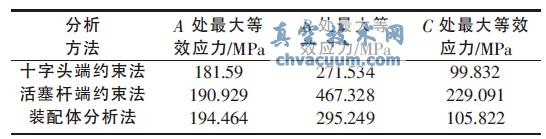
2、介杆应力值的理论计算

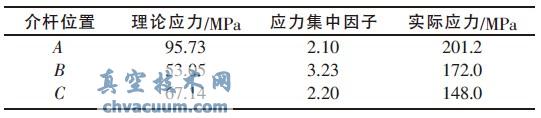
介杆在工作过程中， 主要受到压力的作用，由于A 处、B 处与C 处均为应力集中部位， 故对此3处采用应力集中因子与理论应力值乘积的方法进行实际应力值的计算。计算结果如表2 所示。

表2 介杆理论计算结果

3、结语

本文首先运用有限元分析方法， 基于ANSYS平台，分别用3 种加载方式对介杆进行了有限元计算，然后利用理论计算方法依次计算了介杆A、B、C处的应力值。通过对比各个计算结果，可以看出活塞杆端约束法与其他算法的计算结果相差较大。综合计算效率、计算准确性等因素，建议采用十字头端约束的有限元分析法。